Einige Möglichkeiten, wie wir kausale Effekte mithilfe von maschinellem Lernen , Statistik und Ökonometrie modellieren können, von einem religiösen Text aus dem sechsten Jahrhundert bis zum kausalen maschinellen Lernen von 2021 einschließlich kausaler Verarbeitung natürlicher Sprache .
Stellen Sie sich vor, Sie erhalten einen Datensatz von Schülern und ihren Studienwegen im Laufe der Zeit und möchten herausfinden, ob eine Karriere-Coaching-Intervention sinnvoll ist ein Student, der mit mehr oder weniger hoher Wahrscheinlichkeit eine Universität besuchen wird.
Sie analysieren den Datensatz und können einige Zusammenhänge erkennen. Möglicherweise besuchen bestimmte Untergruppen von Studierenden eine Universität, nachdem sie eine Intervention erhalten haben, und bei einigen Gruppen scheint die Wahrscheinlichkeit, dass sie eine Universität besuchen, wenn sie die Intervention erhalten haben, geringer zu sein.
Der Haken ist, dass Studierende, die sich für Coaching interessierten, möglicherweise sowieso daran interessiert waren, eine Universität zu besuchen. Oder vielleicht hat die Schule nur für Schüler angeboten, bei denen das Risiko besteht, dass sie ihre Ausbildung abbrechen , vielleicht für diese Schüler aus einkommensschwächeren Verhältnissen?
Bei beiden Möglichkeiten beeinflussten das Interesse, die Eignung oder der sozioökonomische Status des Studenten die Chancen, ein Karriere-Coaching zu erhalten, und beeinflussen auch die Chancen, eine Universität zu besuchen. Ein solcher externer Faktor wird als „Confounder“ bezeichnet. Wie können Sie feststellen, ob das Karriere-Coaching die Entscheidung eines Studenten für ein Studium beeinflusst hat, wenn es einen Störfaktor gibt, der sowohl die Entscheidung für ein Karriere-Coaching als auch die Wahrscheinlichkeit, sich für ein Studium zu entscheiden, beeinflusst?
 can influence the choice to deliver an intervention, but can also directly influence the effectiveness of the intervention. How can we untangle this to discover causal relationships between the intervention and the final outcome?](https://fastdatascience.com/images/causal-machine-learning-confounders-on-career-coaching-2-min.png)
Faktoren wie der sozioökonomische Status und die akademische Leistung können die Entscheidung für die Durchführung einer Intervention beeinflussen, können aber auch direkt die Wirksamkeit davon beeinflussen der Eingriff. Wie können wir dies entwirren, um kausale Zusammenhänge zwischen der Intervention und dem Endergebnis zu entdecken?
Selbst bei einem großen, sauberen und ansonsten idealen Datensatz kann es sehr schwierig sein, kausale Auswirkungen zu identifizieren. Der Kausalschluss ist mit Schwierigkeiten verbunden.
Herkömmliche Techniken des Lernens basieren auf der Identifizierung von Korrelationen und der Vorhersage von Ergebnissen auf der Grundlage von Mustern in vergangenen Daten. Beispielsweise kann ein sehr einfaches Modell für maschinelles Lernen, etwa ein logistisches Regressionsmodell , trainiert werden, um die Wahrscheinlichkeit vorherzusagen, mit der ein hypothetischer Student eine Universität besuchen wird. Informationen darüber, ob sie eine Intervention erhalten haben oder nicht. Wenn die Intervention jedoch mit der Begabung und dem sozioökonomischen Hintergrund des Schülers verknüpft ist, sagt uns das Modell des maschinellen Lernens möglicherweise nicht viel.
Wenn Sie entweder traditionelles nichtkausales maschinelles Lernen oder Statistiken verwenden, können Sie sogar seltsame Effekte feststellen, wie zum Beispiel die folgenden:
Dieser Effekt kommt überraschend häufig vor und ist als Simpsons Paradoxon bekannt. Modelle, die die Kausalität nicht berücksichtigen, sind anfällig für diese Art der Fehlinterpretation von Daten.
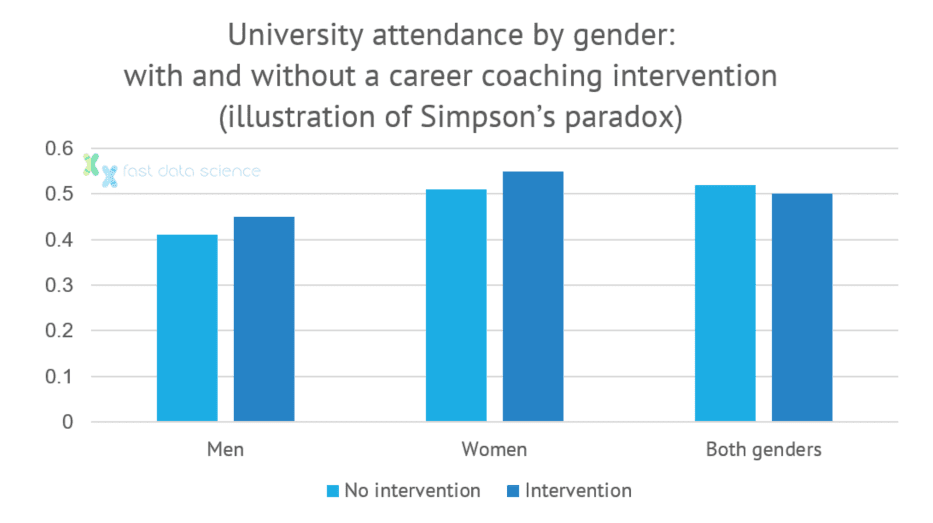
Ein Beispiel für das Simpson-Paradoxon: Eine Intervention scheint einen negativen Effekt zu haben, wenn wir beide Geschlechter zusammen betrachten, aber wenn wir jedes Geschlecht isoliert betrachten, hat die Intervention einen positiven Effekt.
Wenn Sie die Anzahl der an das Modell übergebenen Karriere-Coaching-Interventionen erhöhen, wird ein hypothetischer Student simuliert, der mehr Interventionen erhalten hat, aber implizit hat dieser fiktive Student jetzt einen anderen sozioökonomischen Hintergrund und war schon vor dem Modell mit mehr oder weniger hoher Wahrscheinlichkeit an der Universität Intervention hat stattgefunden!
Unabhängig davon, ob wir nur eine Grafik unserer Daten betrachten, Zahlen durchforsten oder ein Modell für maschinelles Lernen erstellen, wird das Ergebnis dasselbe sein: Wir wissen nicht, inwieweit und in welchem Ausmaß ein Unterschied in den Ergebnissen der Schüler auf eine Intervention zurückzuführen ist es liegt am Hintergrund des Schülers.
Weitere analoge Beispiele für das obige Problem sind:
Wir möchten anhand eines Datensatzes von einigen tausend Patienten herausfinden, ob eine medizinische Behandlung zur Genesung geführt hat. Patienten, die sich für die Behandlung entscheiden, sind jedoch tendenziell in einem schlechteren Zustand als diejenigen, die dies nicht tun.
In diesem Fall ist der anfängliche Gesundheitszustand des Patienten ein Störfaktor. Wenn wir uns nur die Kohorten von Patienten mit und ohne Behandlung ansehen, scheinen sich diejenigen ohne Behandlung besser erholt zu haben, was den Eindruck erweckt, dass die Behandlung eher schädlich als nützlich war.
Unten können Sie ein reales Beispiel des Simpson-Paradoxons aus einer 1986 in London durchgeführten Studie über Nierensteine testen [14] . Die Forscher wollten herausfinden, welche der beiden Behandlungen von Nierensteinen eine bessere Heilungsrate hatte. Das Paradoxe besteht darin, dass Behandlung B wirksamer zu sein scheint, wenn wir beide Größen von Nierensteinen zusammen betrachten, während Behandlung A eine bessere Heilungsrate aufweist, wenn wir beide Größen isoliert betrachten. Durch Anpassen der Zahlen können Sie das Verhältnis ändern und herausfinden, welche Zahlen das Simpson-Paradoxon erscheinen oder verschwinden lassen.
Wenn die Wahrscheinlichkeit, dass eine Intervention durchgeführt wird (Berufscoaching, medizinische Behandlung), durch Störfaktoren beeinflusst wird, die außerhalb unserer Kontrolle liegen, gibt es eine Reihe statistischer Techniken aus mehreren Disziplinen, um die Störfaktoren zu berücksichtigen.
Der einzig sichere Weg, Störfaktoren zu eliminieren, ist jedoch der „Goldstandard“, der in der pharmazeutischen -Industrie verwendet wird, nämlich die randomisierte kontrollierte Studie . Ein Pharmaunternehmen möchte wissen, ob Medikament A besser ist als Medikament B. Wenn es den Patienten die Wahl lässt, welches Medikament sie erhalten, sind sie den Auswirkungen von Störfaktoren ausgesetzt. Wenn Sie jedoch würfeln und Patienten nach dem Zufallsprinzip einer der beiden Behandlungen zuordnen, können Sie die beiden Kohorten A und B vergleichen und wissen, dass etwaige Unterschiede in den Ergebnissen ausschließlich auf die bereitgestellte Behandlung zurückzuführen sind, sofern die beiden Gruppen groß genug sind.
Um eine randomisierte kontrollierte Studie in irgendeinem Bereich durchzuführen, sei es über Pharmazeutika , Karriere-Coaching oder einen anderen Bereich, ist ein Ideal und oft erforderlich unerreichbare Situation:
Im wirklichen Leben stehen wir häufig vor einem Datensatz, der bereits erhoben wurde (z. B. die oben erwähnten Schülerdaten), oder wir können als Beobachter das Geschehen beobachten, aber nicht eingreifen: Wir können keine Behandlungen anordnen.
Für diese heiklen, aber sehr häufigen Situationen haben Forscher verschiedener Disziplinen eine Reihe statistischer Tricks entwickelt, um Störfaktoren zu beseitigen oder zu berücksichtigen und kausale Zusammenhänge aufzudecken. Allerdings sollte ich betonen, dass die randomisierte kontrollierte Studie allen diesen Techniken überlegen ist.
Donald Rubin and I once made up the motto
NO CAUSATION WITHOUT MANIPULATION
to emphasize the importance of this restrictionPaul Holland, influential statistician, in a 1986 paper[7]
Eine einfache und nicht sehr ausgefeilte Möglichkeit, den Effekt eines Störfaktors zu beseitigen, besteht darin, die Daten zu segmentieren. Am Beispiel der akademischen Ergebnisse des Studenten könnten wir separate Analysen durchführen oder einfach nur Diagramme für Studenten in verschiedenen wirtschaftlichen und akademischen Gruppen erstellen und versuchen herauszufinden, ob Karriere-Coaching-Interventionen mit dem Universitätsbesuch von Studenten aus benachteiligten Verhältnissen mit guten Noten korrelieren in der Schule.
Das Problem bei diesem Ansatz besteht darin, dass die segmentierten Datensätze möglicherweise zu klein sind, um eine sinnvolle Analyse durchzuführen, und dies ist schwierig, wenn die Störvariable kontinuierlich und nicht diskret ist. Darüber hinaus verlieren Sie die statistische Aussagekraft, die Sie mit dem größeren vollständigen Datensatz erreichen würden.
Sie müssen auch über den Störfaktor Bescheid wissen und über Daten dazu verfügen, um ihn segmentieren zu können. Daher können wir nicht segmentieren, wenn der Störfaktor unbekannt ist (wenn wir keine Daten darüber haben, ob die Schüler in unserem Datensatz aus Alleinerziehenden oder Kerneltern stammen). Familien können wir dies nicht segmentieren, um es als Störfaktor zu entfernen).
Ein anderer Ansatz zur Beseitigung von Störfaktoren besteht darin, jeden Schüler, der eine Intervention erhalten hat, mit einem Schüler mit einem ähnlichen finanziellen und schulischen Hintergrund zu vergleichen, der die Intervention nicht erhalten hat. Es gibt eine Reihe statistischer Techniken, mit denen wir Übereinstimmungen berechnen können, z. B. Propensity Score Matching . Der Abgleich kann jedoch arbeitsintensiv und unflexibel sein und tatsächlich Voreingenommenheit aufgrund von Störfaktoren.
In bestimmten Bereichen wie Wirtschaftswissenschaften, Soziologie oder Politikanalyse ist es selten, dass ein Forscher die Möglichkeit hat, eine richtige experimentelle Studie wie eine randomisierte kontrollierte Studie durchzuführen. Seit den 1930er Jahren müssen Forscher in den Sozialwissenschaften statistische Methoden anwenden, um Kausalitäten zu identifizieren.
Wenn es einen Faktor gibt, der die Zuweisung einer Intervention beeinflusst und von dem Sie glauben, dass er teilweise zufällig ist oder keinem unterliegt , können Sie so tun, als hätten Sie einen randomisierten Eingriff durchgeführt Kontrollierter Versuch. Ein Experiment wie dieses ohne echten Eingriff wird als Quasi-Experiment bezeichnet.
Eine besondere Art von Quasi-Experiment , das seit den 1930er Jahren verwendet wird, aber in den 1980er Jahren in der Ökonometrie populär wurde, ist Schätzung instrumenteller Variablen .
Stellen wir uns am Beispiel unserer Karriere-Coaching-Intervention vor, dass wir über einen Datensatz verfügen, der nicht nur alle durchgeführten Karriere-Coaching-Interventionen enthält, sondern auch diejenigen Interventionen, die geplant waren, dann aber aufgrund der Sperrungen (oder anderer Gründe) abgesagt wurden Faktor, der außerhalb der Kontrolle der Schüler liegt).
Ich glaube nicht, dass es hinsichtlich der Motivation oder des sozioökonomischen Hintergrunds einen Unterschied zwischen zwei Studenten geben würde, deren Karriere-Coaching-Sitzungen im Abstand von einer Woche geplant waren, eine vor und eine nach dem 26. März 2020 (dem Datum des ersten Lockdowns in England).
Die Absage oder Nichtabsage einer Karrieresitzung ist daher eine Variable, die nicht mit unseren Störfaktoren korreliert. Dies wird unsere instrumentelle Variable genannt.
Die instrumentelle Variable gibt uns die Möglichkeit, zwei Studierende zu vergleichen, bei denen wir wissen, dass die Intervention zumindest teilweise durch den uns bekannten quasi-zufälligen Faktor beeinflusst wurde.
Eine instrumentelle Variable muss in einem Quasi-Experiment einen direkten Einfluss auf die unabhängige Variable haben, aber keinen direkten Einfluss auf die abhängige Variable.
Einige sehr gute Kandidaten für instrumentelle Variablen , die Ihnen bei der Durchführung eines Quasi-Experiments helfen können, sind Effekte, die ihren Ursprung in:
Unsere instrumentelle Variable muss ein Wert sein, der Einfluss darauf hat, ob der Student an einer Berufsberatung teilgenommen hat, der aber keinen direkten Einfluss auf seine Entscheidung für ein Studium hat.
Unsere instrumentelle Variable muss beeinflussen, ob eine Intervention durchgeführt wird, kann aber das Ergebnis nicht direkt beeinflussen.
Der sozioökonomische Hintergrund des Studenten ist kein geeigneter Kandidat für eine instrumentelle Variable, da er sich direkt auf die Chancen des Studenten auswirkt, eine Universität zu besuchen, mit oder ohne Berufscoaching.
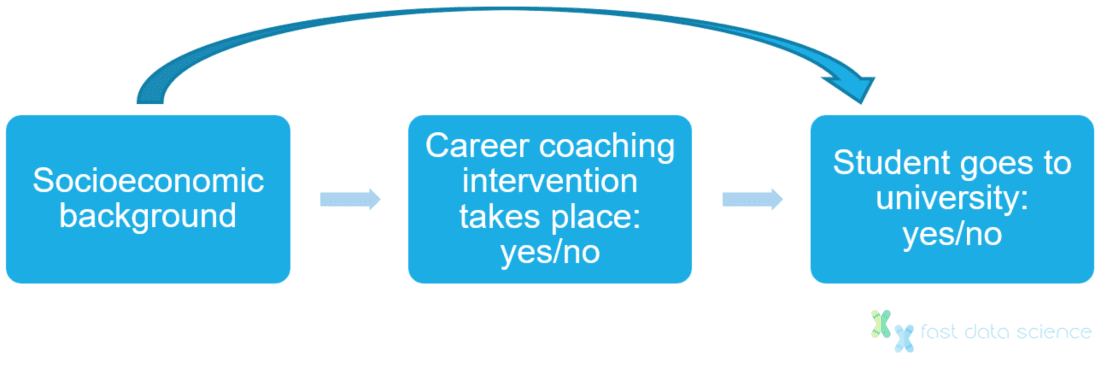
Wir können den sozioökonomischen Hintergrund nicht als Instrument verwenden, da er unabhängig von der Intervention auch einen direkten Einfluss auf die Studienwahl hat.
Der Covid-Lockdown wirkt sich vermutlich auf die Chancen eines Studenten aus, eine Universität zu besuchen, aber ich könnte mir vorstellen, dass, wenn man einen Datensatz von Studenten mit geplanten Terminen im März 2020 nehmen würde, das Datum der Karrieren, die innerhalb oder außerhalb der Lockdown-Daten liegen, genauso gut wäre als zufällig.
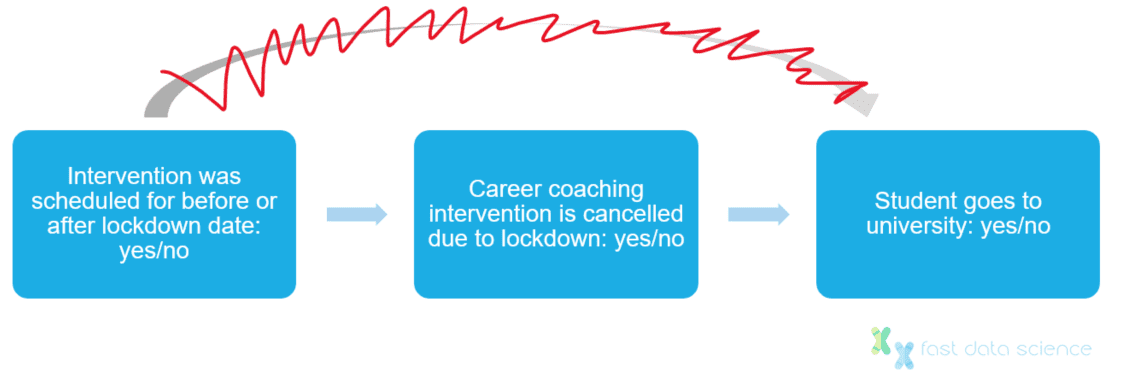
Wir können davon ausgehen, dass ein für März 2020 geplanter Eingriff abgesagt würde, wenn er unter einen Lockdown fallen würde. Dieser Effekt steht in keinem Zusammenhang mit den akademischen Fähigkeiten oder Finanzen der Studierenden und hat keinen direkten Einfluss auf den Universitätsbesuch.
Interventionen, die unter den Lockdown fallen, sind daher eine geeignete instrumentelle Variable.
Der babylonische Talmud wurde im sechsten Jahrhundert geschrieben und beschränkte die Klassengröße auf 40 Schüler. Bildquelle: Wikimedia .
וְאָמַר רָבָא סַךְ מַקְרֵי דַרְדְּקֵי עֶשְׂרִין וְחַמְשָׁה יָנוֹקֵי וְאִי אִיכָּא חַמְשִׁין מוֹתְבִינַן תְּרֵי וְאִי אִיכָּא אַרְבְּעִין מוֹקְמִינַן רֵישׁ דּוּכְנָא וּמְסַיְּיעִין לֵיהּ מִמָּתָא
And Rava said: The maximum number of students for one teacher of children is twenty-five children. And if there are fifty children in a single place, one establishes two teachers, so that each one teaches twenty-five students. And if there are forty children, one establishes an assistant, and the teacher receives help from the residents of the town to pay the salary of the assistant.Bava Batra (“The Last Gate”), Babylonian Talmud (Jewish sacred text completed in 6th Century AD)
Maimonides war ein jüdischer Gelehrter, der im 12. Jahrhundert in Spanien lebte. Er interpretierte das obige Zitat aus dem babylonischen Talmud als Anweisung, alle Schulklassen auf 40 Schüler zu beschränken.
Gemäß Maimonides-Regel muss jede Klasse, die mehr als 40 Schüler hat, aufgeteilt werden, sodass aus einer Kohorte von 41 Schülern eine Klasse mit 20 und eine weitere Klasse wird von 21 Studierenden. Die Klassengrenze von 40 Studenten wurde im modernen Israel zu Rechtswissenschaften erklärt.
Im Jahr 1999 wollten die Ökonomen Joshua Angrist und Victor Lavy die Auswirkung der Klassengröße auf die Lesefähigkeit israelischer Kinder messen, stießen jedoch auf den verwirrenden Faktor, dass die Klassengröße mit sozioökonomischen Gruppen korreliert. Wohlhabendere Eltern haben tendenziell die Möglichkeit, ihre Kinder auf Schulen mit einem besseren Lehrer-Schüler-Verhältnis zu schicken.
Offensichtlich würde kein Elternteil zustimmen, dass sein Kind an einer randomisierten kontrollierten Studie mit unterschiedlichen Klassengrößen teilnimmt. Daher beschränkten sich Angrist und Lavy auf eine beobachtende (nicht-interventionelle) Studie, standen jedoch vor der Herausforderung, den kausalen Effekt der Klassengröße auf das Lernergebnis von dem kausalen Effekt des Hintergrunds der Eltern auf das Lernergebnis zu trennen Der Hintergrund der Eltern und die Klassengröße korrelierten miteinander.
Die Problemumgehung von Angrist und Lavy bestand darin, alle Klassen der Klassen 40, 20 und 21 zu nehmen und davon auszugehen, dass die Klassengrößen um diese Werte herum zufällig sind, da niemand vorhersagen kann, ob in einem bestimmten Jahr 40 oder 41 Kinder eingeschrieben werden. Sie waren daher in der Lage, die Leseverständniswerte von Kindern in sehr kleinen und sehr großen Klassen zu vergleichen, wobei sie wussten, dass die Klassengröße selbst unabhängig vom wirtschaftlichen und Bildungshintergrund der Eltern und anderen Störfaktoren war.
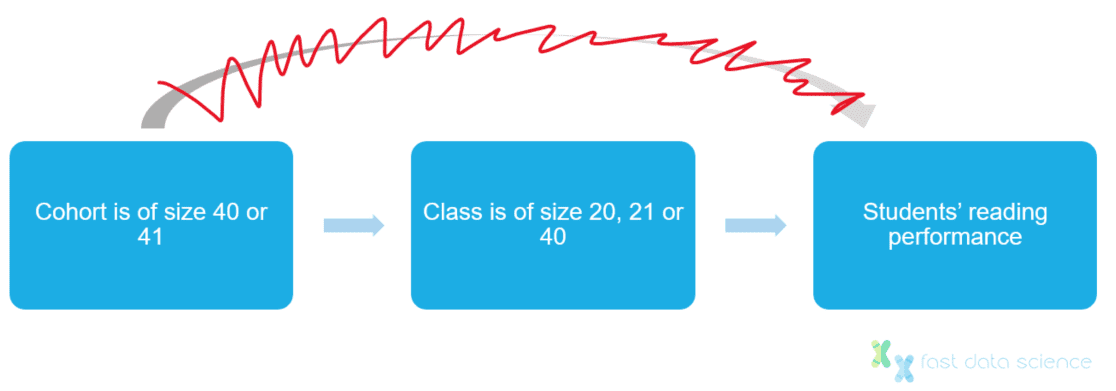
Kohortengrößen um den legalen Schwellenwert von 40 haben nichts mit dem sozioökonomischen Hintergrund der Eltern zu tun, haben keinen direkten Einfluss auf die Lernergebnisse und können daher verwendet werden als instrumentelle Variable.
Mit diesem cleveren Trick konnten Angrist und Lavy die Nebenwirkungen einer Verwaltungsvorschrift nutzen und eine Analyse fast so durchführen, als hätten sie eine randomisierte kontrollierte Studie durchgeführt. Dies ist ein elegantes Beispiel dafür, wie Kausalität manchmal auch dann abgeleitet werden kann, wenn der Forscher nicht in der Lage ist, ein Experiment durchzuführen.
Joshua Angrist arbeitete an einer anderen Arbeit, in der er die Auswirkungen des Kriegsdienstes im Vietnamkrieg auf das Lebenseinkommen untersuchte. Hier stieß er auf ein ähnliches Problem: Menschen mit einem höheren Bildungsniveau melden sich seltener freiwillig zum Militär und haben tendenziell auch ein hohes Durchschnittseinkommen, unabhängig davon, ob sie beim Militär dienen oder nicht.
Glücklicherweise führte die US-Regierung eine Reihe von Draft-Lotterien durch, bei denen Männer nach einem Zufallsverfahren für den Kriegseinsatz rekrutiert wurden: ein idealer Kandidat für eine instrumentelle Variable. Durch die Kenntnis des Anteils freiwilliger Rekruten, Kriegsdienstverweigerer und Menschen, die aus medizinischen Gründen abgelehnt wurden, konnte Angrist einen Einkommensrückgang von 15 % für weiße Veteranen im Vergleich zu Nichtveteranen schätzen.
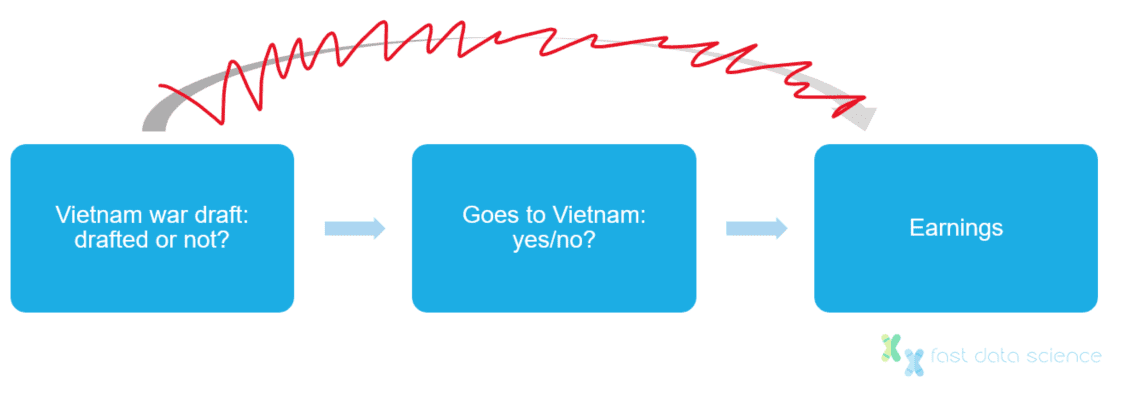
Die Draft-Lotterie ist zufällig und hat nur einen direkten Einfluss darauf, ob eine Person nach Vietnam geht oder nicht, hat aber keinen direkten Einfluss auf das Einkommen. Daher könnte die Wehrpflicht als Instrumentvariable genutzt werden, um den störenden Faktor zu beseitigen, dass hochgebildete Menschen nicht dazu neigen, sich zum Militär zu melden.
Die oben beschriebenen Ansätze stammen überwiegend aus den Bereichen Statistik und Wirtschaftswissenschaften. Allerdings ist maschinelles Lernen als Feld im Allgemeinen nicht kausal und befasst sich mit immer intelligenteren Assoziationen oder Korrelationen zwischen Dingen. Beispielsweise kann ein hochmodernes neuronales Netzwerk Bilder in verschiedene Hunderassen klassifizieren oder vorhersagen, was ein Kunde ausgeben wird, versucht aber nicht, das Warum anzusprechen. : Was es ist, das einen Kunden dazu bringt, mehr oder weniger auszugeben.
Im Laufe der Jahre gab es eine Reihe von Versuchen, kausale Modelle für maschinelles Lernen zu entwickeln oder Kausalität in bestehende Frameworks einzuführen. Bei vielen kausalen KI-Mechanismen wird ein Diagramm erstellt, das zeigt, wie Ereignisse einander verursachen. Eines der bekanntesten Frameworks sind Bayes’sche Netzwerke:
Die Informatikerin Judea Pearl entwickelte eine ausgeklügelte Methode zur Darstellung kausaler Zusammenhänge in einem gerichteten Graphen, dem sogenannten Bayes’schen Netzwerk. [11] Pfeile werden gezeichnet, wenn zwischen zwei Knoten des Diagramms ein kausaler Zusammenhang besteht, obwohl die beobachtete statistische Korrelation nicht von der Richtung des Pfeils abhängt. Bayesianische Netzwerke sind in der Lage, Konzepte aus der Ökonometrie wie instrumentelle Variablen darzustellen.
Pearl entwickelte außerdem die „Do-Kalküle“, bei der unterschieden wird zwischen der Wahrscheinlichkeit, dass ein Student eine Universität besucht, wenn eine Karriere-Coaching-Intervention durchgeführt wurde:
P(Student besucht die Universität | Student hat eine Intervention erhalten)
und die Wahrscheinlichkeit, dass der Student die Universität besucht hat, vorausgesetzt, wir (der Experimentator) haben eine Intervention erzwungen:
P(Student besucht die Universität | do(Student hat eine Intervention erhalten))
Bayesianische Netzwerke sind leistungsstark, weil sie sehr komplexe Beziehungsnetzwerke darstellen können. Sie werden in Bereichen wie der Medizin eingesetzt, um darzustellen, wie Symptome und Krankheiten miteinander verknüpft sind. Das folgende Netzwerk zeigt beispielsweise ein Bayesianisches Modell zur Vorhersage der -Krankheit .
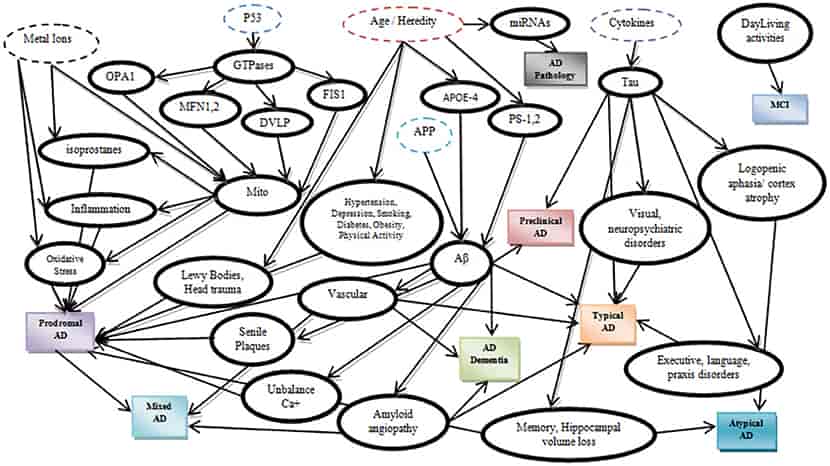
Ein Bayesianisches Netzwerk, das die kausalen Zusammenhänge im Zusammenhang mit der Alzheimer-Krankheit zeigt. Bildquelle: [1]
Es ist auch möglich, eine Bayes’sche Netzwerkstruktur zu erlernen. Beispielsweise kommen im Körper Tausende von Proteinen und Genen gleichzeitig vor. Es ist schwierig, die Ursache-Wirkungs-Ketten zu erraten, aber mithilfe statistischer Methoden konnten wir die Struktur von Bayes’schen Netzwerken erlernen und kausale Zusammenhänge erraten.
Einige Epidemiologen führten 2012 eine Studie durch, in der sie die Ursachen von Durchfall bei Kindern in Pakistan untersuchten [8] . Traditionelle Statistiken deckten 12 Variablen auf, die mit Durchfall in Zusammenhang standen, darunter die Anzahl der Räume im Haushalt. Das war schwer zu interpretieren. Eine Analyse mit einem kausalen Bayes’schen Netzwerk konnte jedoch eine Netzwerkkarte mit drei Variablen zeigen, die das Auftreten von Durchfall direkt beeinflussten: keine formelle Müllabfuhr, Zugang zu einer Trockengrubenlatrine und Zugang zu einer atypischen anderen Wasserquelle. Die Erkenntnisse aus der Studie könnten einen enormen gesellschaftlichen Nutzen bringen, wenn sie in die Politik einfließen.
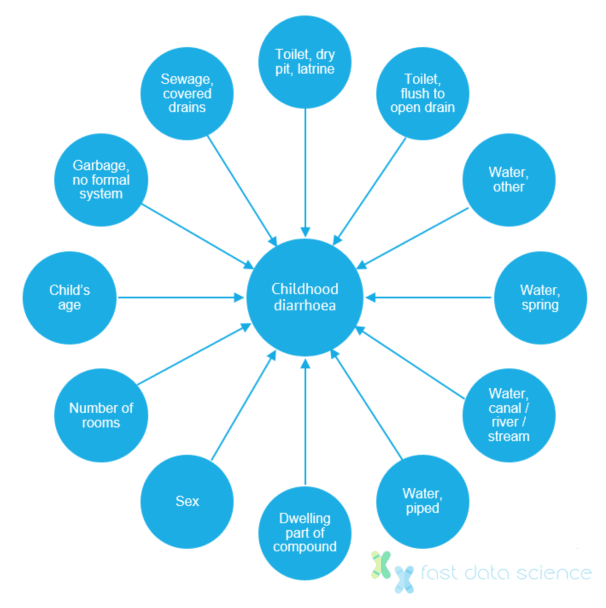
Diagramm, das die Korrelationen zwischen anderen Faktoren und der Häufigkeit von Durchfall bei Kindern zeigt. Mithilfe des Bayes’schen Netzwerkansatzes konnten die Epidemiologen drei wahrscheinliche ursächliche Faktoren für Durchfall identifizieren: keine formelle Müllabfuhr, Zugang zu einer trockenen Grubenlatrine und Zugang zu einer atypischen anderen Wasserquelle. Bild angepasst von [8] .
Die großen Datenmengen, die von Technologiegiganten wie Facebook und Google gesammelt wurden, ebneten den Weg für die Einführung von tiefen neuronalen Netzen für Zwecke in Branchen , während in der Wissenschaft Projekte wie das 1000 Genomes Project haben über zweihundert Terabyte an Informationen gesammelt [12] . Wenn wir fragen möchten, wem wir jemanden empfehlen sollten, mit dem wir uns in einem sozialen Netzwerk verbinden sollten, oder herausfinden möchten, welches Gen mit einer bestimmten Krebsart assoziiert ist, können wir modernste Modelle des maschinellen Lernens wie neuronale Netze einsetzen, um Assoziationen in den Daten zu ermitteln.
Allerdings ist der Zusammenhang eines Gens mit Krebs keine kausale, sondern eine statistische Frage. Deep Neural Networks sind hochentwickelt und leistungsstark, aber einige der Hype um sie herum ignoriert die Tatsache, dass sie sich normalerweise nicht mit kausalen Fragen befassen. Kausalfragen können nicht allein durch Daten beantwortet werden, sondern erfordern ein Modell der datengenerierenden Prozesse.
Wir können beispielsweise ein Modell konstruieren, das angibt, dass ein Gen die Krebsanfälligkeit einer Person beeinflussen kann, umgekehrt jedoch nicht. Allerdings müssten wir die Möglichkeit von Störfaktoren wie einem Mediator in Betracht ziehen (das Gen beeinflusst ein Verhalten wie Rauchen, das wiederum das Krebsrisiko erhöht). Die Werkzeuge der Ökonometrie oder der Bayes’schen Netzwerke können an diese Art von Modell angepasst werden, was ein reales Verständnis davon erfordert, was was beeinflussen kann.
In manchen Fällen ist es möglich, die zeitliche Abfolge von Ereignissen zu nutzen, um kausale Zusammenhänge herauszufinden. Wenn ein Student eine Karriereintervention erhält und dann ein Jahr später die Universität besucht, bedeutet das, dass der Universitätsbesuch keinen Einfluss auf die Karriereintervention haben kann. Eine beliebte Methode zur Verwendung von Zeitreihen ist die sogenannte Granger-Kausalität, die die Zeit verschiedener Ereignisse nutzt und bestimmt, welches Ereignis das andere Ereignis besser erklärt.
Reinforcement learning is a field of AI that is used to learn interactions with an environment, such as a chess-playing AI or a self-driving car. An AI is considered an ‘agent’ which can take actions that result in a reward. The reinforcement learning algorithm allows the agent to sometimes take the optimal action (take the knight) but sometimes to ‘explore’ (take a lower value piece) with an aim of learning a better strategy for the future. Although in a sense reinforcement learning is inherently causal, there have been recent modifications to reinforcement learning algorithms to incorporate the sophistication of Bayesian networks to handle confounders and other effects.
Mein besonderes Interessengebiet ist Verarbeitung natürlicher Sprache ( NLP , und ich werde ein wenig darüber schreiben, wie wir NLP in der Kausalität.
Die meisten in der Industrie eingesetzten NLP -Anwendungen werden zur Erstellung von Vorhersagen verwendet. Wie hoch ist zum Beispiel angesichts des Lebenslaufs eines Arbeitssuchenden das wahrscheinlichste Gehalt dieser Person? An welche Abteilung soll eine eingehende E-Mail weitergeleitet werden?
Es gibt jedoch keinen Grund, warum die Variablen in einem Ursache-Wirkungs-Szenario numerisch sein müssen. Ein Textfeld könnte als Ursache für ein numerisches Feld dienen, sich als Wirkung manifestieren oder sogar als Instrumentvariable verwendet werden.
Ein Vorhersagemodell zur Zuordnung von Arbeitssuchenden zu Gehaltsgruppen würde einen Zusammenhang zwischen beiden entdecken. Aber hat die Formulierung Ihres Lebenslaufs Einfluss auf Ihr Gehalt, oder sind der Inhalt des Dokuments und die Höhe des Gehalts das Ergebnis einer gemeinsamen Ursache, beispielsweise jahrelanger Erfahrung? In diesem Bereich ist ein gewisses Maß an Experimenten möglich. Im Jahr 2004 schickten Marianne Bertrand und Sendhil Mullainathan gefälschte Lebensläufe an Arbeitgeber in Boston und Chicago, wobei sie zufällig Namen zuordneten, die afroamerikanisch oder weiß klangen. Sie stellten fest, dass die weißen „Kandidaten“ 50 % mehr Rückrufe für Vorstellungsgespräche erhielten. [5] Wenn jedoch ein Kausalmodell an Textfelder angepasst werden kann, können wir aus Beobachtungsdaten lernen, anstatt Interventionen durchführen zu müssen.
Ein Beispielfall, in dem wir die Kausalität verstehen möchten, wobei die Ursache ein Textfeld ist, ohne ein Experiment durchzuführen, ist wie folgt:
Users post comments on an online forum. Every user has a gender icon on their profile: ♂ or ♀. Users labelled ♀ tend to receive fewer likes. Are the fewer likes due to the icon, or due to the content of the text?[6]
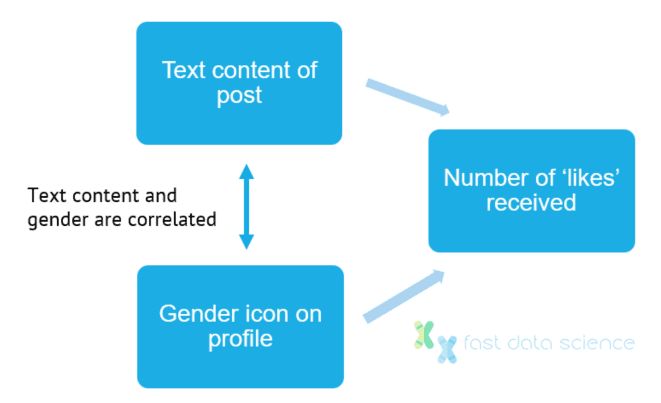
Es ist schwierig, die Wirkung des Profilsymbols von einer Eigenschaft des Textinhalts zu trennen, da beide vom Geschlecht des Benutzers beeinflusst werden. Kausale Techniken des maschinellen Lernens können die Ideen hinter instrumentellen Variablen verallgemeinern, um Störfaktoren zu beseitigen.
Es gibt eine Reihe von Lösungen für diese Art von Problem.
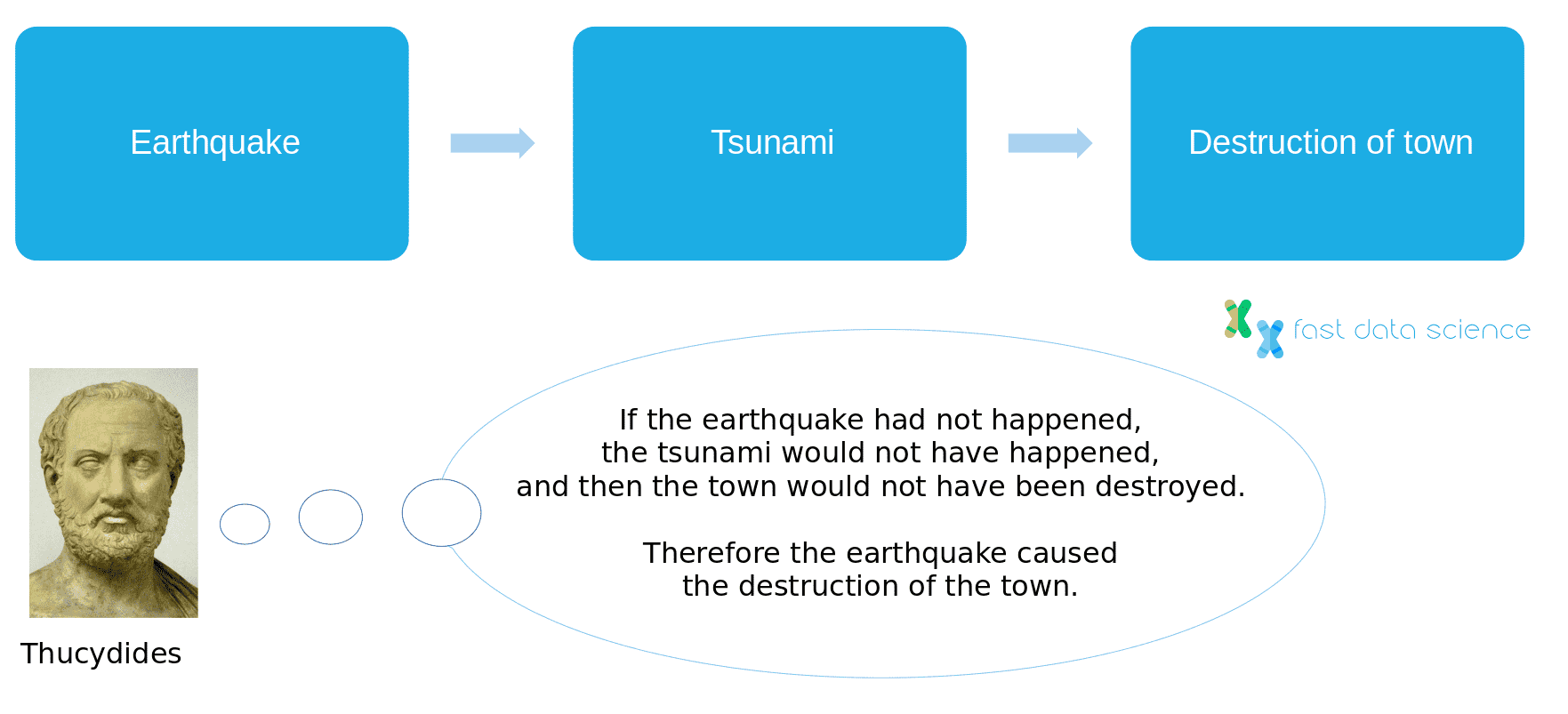
Ich empfehle die Lektüre von _The Book of Why [ _ 12] von Judea Pearl, das sich aus vielen Blickwinkeln mit der Kausalität befasst. Einer der interessanten Punkte, die Pearl hervorhebt, ist, dass wir im Laufe der Geschichte nicht immer eine klare Definition von Kausalität hatten. Beispielsweise beschrieb der griechische Historiker Thukydides einen Vorfall, bei dem ein Erdbeben im Jahr 426 v. Chr. einen Tsunami auslöste, der wiederum eine Stadt zerstörte. Thukydides kam zu dem Schluss, dass das Erdbeben die eigentliche Ursache für die Zerstörung der Stadt gewesen sei
_.
Ohne ein Erdbeben kann ich mir nicht vorstellen, wie ein solcher Unfall passieren könnte.
Geschichte des Peloponnesischen Krieges, Thukydides, frühes viertes Jahrhundert v. Chr. [14]
Dies ist eine Definition einer Ursache: Wir stellen uns ein Paralleluniversum vor, in dem das erste Ereignis nicht stattgefunden hat, und stellen uns vor, was die Folge gewesen wäre. Das imaginäre „Was-wäre-wenn“-Szenario wird als kontrafaktisch bezeichnet.
Kurioserweise definierte der schottische Philosoph David Hume viele Jahrhunderte später Kausalität als den Zusammenhang zwischen zwei Ereignissen, die regelmäßig nacheinander auftreten. Daraus schließen wir, dass eine Flamme Hitze erzeugt, denn jedes Mal, wenn wir eine Flamme sehen, spüren wir Hitze, wenn wir sie berühren. Dies wird als Regelmäßigkeit-Definition der Kausalität bezeichnet.
Neun Jahre später überarbeitete Hume seine Definition der Kausalität von der Regelmäßigkeitsdefinition zurück zur kontrafaktischen Definition und erklärte, dass wir auf Kausalität schließen können, wo
if the first object had not been, the second had never existed
David Hume, Enquiry Concerning Human Understanding[16]
Nach weiteren Überlegungen entschied sich Hume für die Definition der Kausalität durch Thukydides. Heute ist die am weitesten verbreitete Definition von Kausalität die kontrafaktische Definition, obwohl sie viele andere Fragen aufwirft (stellen wir uns ein Universum vor, in dem ein Ereignis nicht stattgefunden hat, aber alles andere identisch war? Welches Universum wählen wir, wenn es mehrere Kandidaten gibt?).
Nachdem ich über die kontrafaktische Definition von Kausalität gelesen hatte, fragte ich mich, warum viele europäische Sprachen unterschiedliche Verbformen verwenden, um Ereignisse, die definitiv nicht stattgefunden haben, von Ereignissen zu unterscheiden, die tatsächlich stattgefunden haben oder stattgefunden haben könnten. Beispielsweise wird im Spanischen mithilfe der Formel eine „Was-wäre-wenn“-Bedingungsanweisung für ein kontrafaktisches Szenario gebildet
si (‘if’) + unvollkommenes Konjunktivverb + Konditionalform
zum Beispiel si no hubiera llovido, no me habría mojado („Wenn es nicht geregnet hätte, wäre ich nicht nass geworden“), wobei hubiera die unvollkommene Konjunktivform des Verbs ist und ein Szenario bezeichnet, das nicht stattgefunden hat. Wenn der Sprecher es für wahrscheinlich oder möglich hält, dass es geregnet hat, würde er „si ha llovido“ sagen und dabei „ha“ anstelle von „hubiera“ verwenden.
Im Englischen neigen wir dazu, die Vergangenheitsform mit had für ein Ereignis zu verwenden, das nicht stattgefunden hat (Kontrafaktuale) und andere Formen wie die Vergangenheitsform mit have für Ereignisse, die tatsächlich stattgefunden haben:
‘if’ + Vergangenheitsform mit had + Konditionalform mit would have
Wir haben also wenn es nicht geregnet hätte, wäre ich nicht nass geworden (es hat nicht geregnet), im Gegensatz zu wenn es nicht geregnet hat, werde ich nicht nass geworden (es hätte vielleicht geregnet). Ein weiteres Beispiel für diese Unterscheidung ist die Verwendung von were in Sätzen wie if I were you oder if he were rich – die Wahl von were anstelle von was in diesen Sätzen zeigt dem Hörer, dass wir uns eine Welt vorstellen, in der jemand reich ist, wer ist nicht reich in unserer Welt.
Auch im Deutschen, Französischen und Italienischen gibt es Konjunktivverbformen, während im Chinesischen unterschiedliche Partikel im Satz verwendet werden, um kontrafaktische und nichtkontrafaktische Bedingungen zu unterscheiden [15] , obwohl die Definition hypothetischer Szenarien spezielle Verbformen erfordert variiert geringfügig von Sprache zu Sprache – nicht alle spanischen Konjunktivsätze erfordern einen Konjunktiv auf Italienisch und umgekehrt. Im Chinesischen sind die kontrafaktischen grammatikalischen Partikel meist optional.
Die Tatsache, dass Kontrafaktuale in die Grammatik unserer Sprachen integriert sind, ist interessant, da sie zeigt, dass Kausalität zwar für uns schwer zu verstehen sein kann (wenn Kausalität leicht zu verstehen wäre, wäre Simpsons Paradoxon kein Paradoxon!), es sich aber um eine intrinsische Eigenschaft handelt Teil unseres Denkens und Kommunizierens.
Kinder im Alter von 6 bis 8 Jahren beherrschen in der Regel die Zeitformen ihrer Muttersprache. Für mich bedeutet das, dass bereits kleine Kinder in der Lage sind, kontrafaktische Zusammenhänge intuitiv zu verstehen und zu begreifen. Im Jahr 2019 führte Keito Nakamichi ein Experiment durch, um genau dies zu untersuchen, und stellte fest, dass Vier- bis Sechsjährige in der Lage sind, über kontrafaktische Ereignisse nachzudenken, die mit emotionalen Ereignissen, aber nicht mit physischen Ereignissen verbunden sind. [17]
Ich habe ein sehr unwissenschaftliches Experiment mit meinen Sechsjährigen durchgeführt und herausgefunden, dass sie kontrafaktische Antworten genau beantworten konnten, aber die Syntax were/would nicht effektiv nutzten und manchmal stattdessen will verwendeten. Sie bildeten ungrammatische Sätze wie „Wenn James‘ Eltern nicht starben, würde er mit ihnen am Meer leben“, was zeigte, dass sie die Kontrafaktuale verstanden, aber die bedingten und konjunktivischen Verbformen nicht beherrschten.
Kausalitätsmodelle werden immer weiter verbreitet und Datenwissenschaftler benötigen zunehmend ein grundlegendes Verständnis der Kausalitätstheorie. Herkömmliche Modelle des maschinellen Lernens konzentrieren sich auf Korrelationen, aber in Fällen wie dem Beispiel der Studierenden, die eine Berufsberatungsmaßnahme erhalten, liefert ein maschineller Lern- oder statistischer Ansatz, der die Kausalität ignoriert, irreführende Ergebnisse, wie zum Beispiel den Eindruck, dass eine Berufswahlmaßnahme eine nachteilige Wirkung hat über einen Studenten, der eine Universität besucht. Wenn die Interventionen selbst auf Schüler abzielen würden, die Gefahr laufen, ihre Ausbildung abzubrechen, wäre diese Schlussfolgerung eindeutig unsinnig.
Es gibt zwei Denkschulen für Kausalmodelle: die älteren Methoden aus der Ökonometrie und den Sozialwissenschaften und die neueren Modelle aus der Informatik wie etwa Bayes’sche Netzwerke. Allerdings kann kein Kausalmodell nicht rein datengesteuert sein, sondern muss so konzipiert sein, dass es das Verständnis seines Erstellers über die vorhandenen Kausalmechanismen berücksichtigt, wie z. B. Einberufung zum Vietnamkrieg ➜ Einberufung in die Armee ➜ Lebensverdienst.
Kausalitätsmodelle werden in den Sozialwissenschaften mindestens seit den 1930er Jahren verwendet, während die Verarbeitung Sprache in der Industrie, insbesondere im letzten Jahrzehnt oder so, aufgrund der Fortschritte bei der Größe von Datensätzen weit verbreitet ist und Rechenleistung. Forscher und Branchenführer fragen sich erst seit Kurzem, wie Kausalität und NLP kombiniert werden können. Die jüngsten Durchbrüche bei immer ausgefeilteren Vektordarstellungen Textdarstellungen und die Verbreitung leicht zugänglicher Textdatensätze bedeuten, dass wir mit einer stärkeren Diskussion über NLP und Kausalität in der Welt rechnen können nahe Zukunft.
Text Mining: Kurzer Überblick Das moderne Unternehmen hat Zugriff auf riesige Mengen unstrukturierter Daten, doch diese Daten können sich nur dann als nützlich erweisen, wenn daraus die gewünschten Erkenntnisse gewonnen werden können.
Wie sieht Textanalyse-KI im Jahr 2023 aus, wie sie generell funktioniert und wie Sie damit Ihre Kunden, Mitarbeiter und Ihre Marke auf das nächste Level heben können – all das und mehr in unserem ausführlichen Artikel.
Natural Language Understanding (NLU): Überblick Wenn wir darüber nachdenken, ist Sprache eines der mächtigsten Werkzeuge in unserem Arsenal. Wir nutzen es, um auszudrücken, was wir fühlen oder denken.
Was wir für Sie tun können
