Tauchen Sie ein in die Welt der Natürlichen Sprachverarbeitung! Entdecken Sie modernste NLP-Rollen, die zu Ihren Fähigkeiten und Leidenschaften passen.
NLP-Jobs entdeckenIn der Verarbeitung natürlicher Sprache gibt es das Konzept der Wortvektoreinbettung und der Satzeinbettung. Dabei handelt es sich um einen Vektor, der normalerweise aus Hunderten von Zahlen besteht und die Bedeutung eines Wortes oder Satzes darstellt.
Einbettungen sind nützlich, weil Sie die Ähnlichkeit zweier Sätze berechnen können, indem Sie beide in Vektoren umwandeln und eine Distanzmetrik berechnen.
Unten sehen Sie, wie zwei Sätze in einen Vektor umgewandelt werden können und wir den Abstand zwischen ihnen messen können.
Das obige Beispiel verwendet den Universal Sentence Encoder lite in Tensorflow JS, der in Ihrem Browser ausgeführt wird und nichts an einen Server sendet. Es verwendet Vektoren der Größe 512 (512-dimensionale Einbettungen).
Wenn Sie vor der Einführung von Einbettungen Dokumente oder Texte vergleichen wollten, um herauszufinden, wie ähnlich sie waren, war es am einfachsten, die gemeinsamen Wörter zu zählen. Dies funktioniert jedoch nicht, wenn Dokumente keine gemeinsamen Wörter aufweisen, sondern Synonyme verwenden. In unserem Blogbeitrag zum Finden ähnlicher Dokumente in NLP können Sie mehr über Möglichkeiten zum Vergleichen von Texten lesen.
Satzeinbettungen bedeuten, dass Ihr gesamter Dokumentsatz in einen Satz von Vektoren umgewandelt und so gespeichert werden kann und jedes neue Dokument schnell mit denen im Index verglichen werden kann.
Im Harmony-Projekt haben wir ein Online-Tool entwickelt, mit dem Psychologen Fragebogenelemente semantisch vergleichen können, um gemeinsame Fragen in Fragebögen zu identifizieren. Harmony berechnet, dass eine Frage wie „Ich bin nervös“ zu 78 % einer Frage wie „Ich bin ängstlich“ ähneln könnte. Dieser Wert ist einfach die Cosinus-Ähnlichkeitsmetrik (die Ähnlichkeit zwischen zwei Vektoren), ausgedrückt als Prozentsatz!
*Sie können die Harmony-App unter harmonydata.ac.uk/app ausprobieren.
Satzeinbettungen werden häufig in Retrieval Augmented Generation (RAG) -Systemen verwendet: Wenn Sie ein generatives Modell wie ChatGPT verwenden, ihm aber domänenspezifisches Wissen geben möchten, können Sie Satzeinbettungen verwenden, um herauszufinden, welcher Teil Ihrer Wissensbasis für die Abfrage eines Benutzers am relevantesten ist.
Wir haben RAG im Projekt Insolvency Bot verwendet, einen Chatbot mit Kenntnissen des englischen und walisischen Insolvenzrechts. Wenn der Benutzer dem Insolvency Bot eine Frage stellt, konvertieren wir diese in eine Einbettung und stellen möglicherweise fest, dass es sich bei der Frage um grenzüberschreitende Insolvenzen handelt. Anschließend senden wir die für grenzüberschreitende Insolvenzen relevanten Teile des Insolvency Act 1986 zusammen mit der Anfrage des Benutzers an OpenAI und erhalten eine Bot-Antwort, die viel besser ist als das, was GPT allein und ohne zusätzlichen Kontext getan hätte.
Zwei der gebräuchlichsten Methoden zum Berechnen der Ähnlichkeit zwischen zwei Satz- oder Wort-Einbettungsvektoren sind die euklidische Distanz und die Kosinus-Ähnlichkeit . Diese sind in zwei Dimensionen leichter zu verstehen.
Stellen wir uns vor, Sie möchten zwei unterschiedliche Sätze und zwei ähnliche Sätze vergleichen. Wenn wir uns vorstellen, dass unsere Vektoren nur zwei statt 512 Dimensionen haben, könnten unsere Sätze wie die folgenden Grafiken aussehen.
Die euklidische Distanz (siehe die beiden Grafiken unten) ist einfach die geradlinige Entfernung zwischen den beiden Vektoren. Sie ist groß, wenn die beiden Sätze sehr unterschiedlich sind, und klein, wenn sie ähnlich sind.
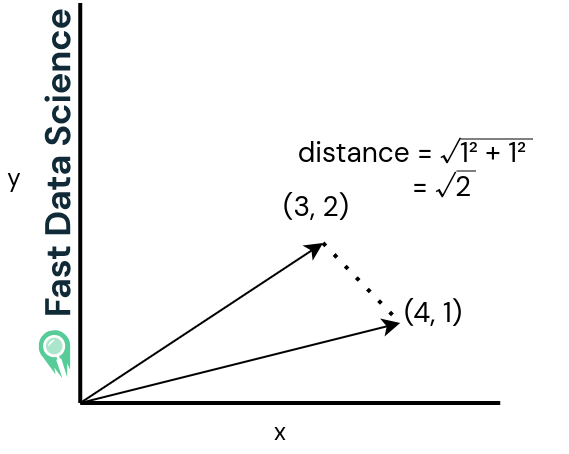
Der euklidische Abstand für zwei nahe beieinander liegende Vektoren ist klein.
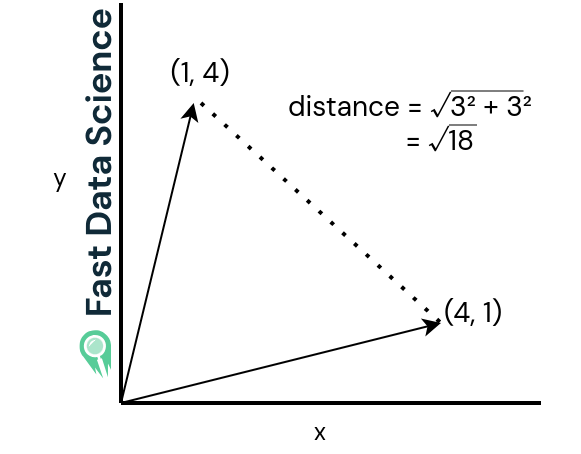
Der euklidische Abstand für zwei Vektoren, die in mehrere unterschiedliche Richtungen zeigen.
Die Kosinusähnlichkeit (untere zwei Graphen) ist ein Wert zwischen -1 und 1 und ist das Skalarprodukt ( Skalarprodukt ) der beiden Vektoren geteilt durch das Skalarprodukt ihrer Längen. Für Vektoren der Länge 1 ist es dasselbe wie das Skalarprodukt der beiden Vektoren (Sie müssen durch nichts dividieren).
Ähnliche Sätze haben eine Kosinusähnlichkeit nahe 1, während sehr unterschiedliche Sätze eine Ähnlichkeit nahe 0 oder sogar negativ haben. Kosinusähnlichkeiten nahe -1 sind ziemlich selten.
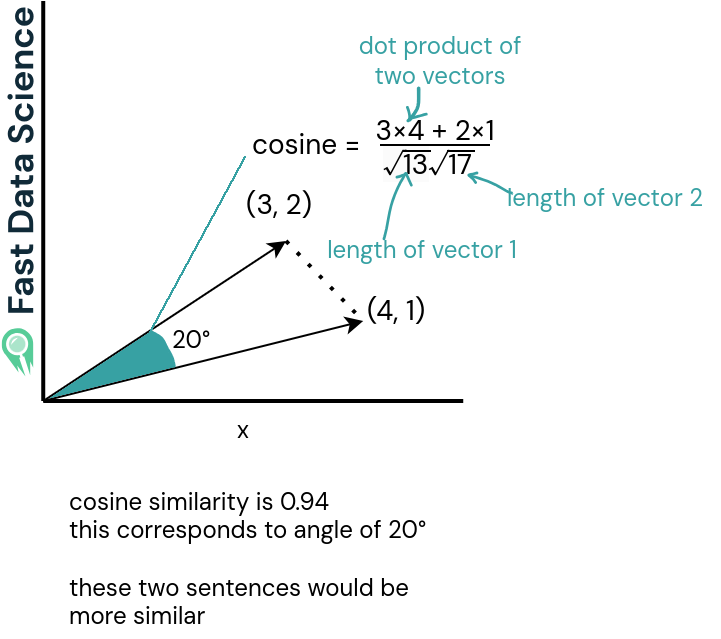
Die Kosinus-Ähnlichkeit ist groß oder nahe 1 für zwei Vektoren, die in eine ähnliche Richtung zeigen, was auf semantische Ähnlichkeit hinweist.
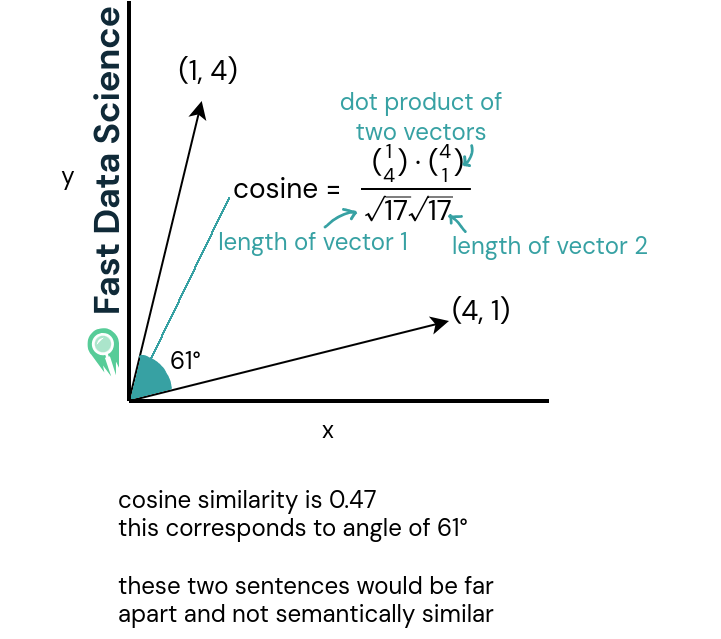
Die Kosinusähnlichkeit ist bei zwei Vektoren, die in sehr unterschiedliche Richtungen zeigen, gering. Bei Vektoren, die in entgegengesetzte Richtungen zeigen, wäre sie negativ.
Die meisten Modelle zur Satzeinbettung, wie etwa die HuggingFace-Transformatormodelle, ergeben alle Vektoren der Länge 1, was bedeutet, dass Sie die untere Hälfte des Bruchs in der Formel für die Kosinus-Ähnlichkeit nicht berechnen müssen.
In der Demonstration oben auf dieser Seite berechnen wir die Kosinus-Ähnlichkeit.
Semantic similarity with NLP
T. Mikolov et al.. Effiziente Schätzung von Wortdarstellungen im Vektorraum , arXiv : 1301.3781 (2013)
Reimers und Gurevych, Sentence-BERT: Satzeinbettungen mithilfe siamesischer BERT-Netzwerke (2019).
Cer et al. Universeller Satzencoder (2018).
Ribary, M., Krause, P., Orban, M., Vaccari, E., Wood, TA, Prompt Engineering und Bereitstellung von Kontext bei der domänenspezifischen Verwendung von GPT , Frontiers in Artificial Intelligence and Applications 379: Rechtliches Wissen und Informationssysteme, 2023. https://doi.org/10.3233/FAIA230979
Suchen Sie Experten in Natürlicher Sprachverarbeitung? Veröffentlichen Sie Ihre Stellenangebote bei uns und finden Sie heute Ihren idealen Kandidaten!
Veröffentlichen Sie einen Job
Generative KI Einführung Generative KI , ein Teilbereich der KI, verändert Branchen grundlegend und gestaltet die Zukunft. Durch die Nutzung fortschrittlicher Algorithmen kann generative KI Inhalte, Designs und Lösungen erstellen, die zuvor undenkbar waren.
Große Daten Das Aufkommen von Big Data hat ganze Branchen revolutioniert und traditionelle Geschäftsmodelle und Entscheidungsprozesse verändert. In dieser umfassenden Untersuchung gehen wir der Frage nach, was Big Data ist, welche erheblichen Auswirkungen es auf die Geschäftsstrategie hat und wie Unternehmen riesige Datenmengen nutzen können, um Innovationen voranzutreiben und sich einen Wettbewerbsvorteil zu verschaffen.
What we can do for you
